迪杰斯特拉(Dijkstra)算法

迪杰斯特拉算法

该算法是典型的最短路径算法，用于计算一个节点到其他节点的最短路径。

主要特点是以起始点为中心向外层层扩展（广度优先搜索思想），直到扩展到终点为止。

起源与历史

来自维基百科：

从鹿特丹到格罗宁根的最短路径是什么？实际上，这就是对于任意两座城市之间的最短路问题。解决这个问题实际上大概只花了我20分钟：一天早上，我和我的未婚妻在阿姆斯特丹购物，累了，我们便坐在咖啡馆的露台上喝咖啡，然后我就试了一下能否用一个算法解决最短路问题。正如我所说，这是一个20分钟的发现。不过实际上，我在3年后的1959年才把这个算法发表在论文上。即使现在来看这篇论文的可读性也非常高，这个算法之所以如此优雅，其中一个原因就是我没用笔纸就设计了它。后来我才知道，没用笔纸设计的优点之一是你不得不避免所有可避免的复杂问题。令我惊讶的是，这个算法最终成为我成名的基石之一。

基本思想

先说明：该问题我们使用的思路实际上是 贪心

首先声明问题：我们要求的是节点 A 到其他节点的最短路径。

定义两个集合 S 和 U，S 集合包含已经求出最短路径的点，U 集合包含还未求出最短路径的顶点。

并且对应创建一个数组 M 用于记录节点 A 到其他节点的距离，在遍历过程中需要对该数组进行更新。

初始时，S 中仅包含起始节点 A，然后此时 M 中的值为，从 A 到其他直接相连的节点的距离（不相连的是 ∞ ）。

然后从数组 M 中找出 S 最新加入的点 P（最开始的话会是起始点 A）距离最近的点 Q ，将其放入到集合 S 中，然后用直接与 Q 相连且最近的节点 R 的距离更新数组 M（如果此时 A 到 R 的直接相连距离「此时记录在数组中」大于 A 到 Q 的距离加上 Q 到 R 的距离，则更新数组 M 中，关于 A 到 R 的距离的数据）。

然后依次循环上方进行的步骤，直到遍历完成所有的点，此时数组数据就是我们需要的节点 A 到其他节点的最短路径。

逻辑运行图

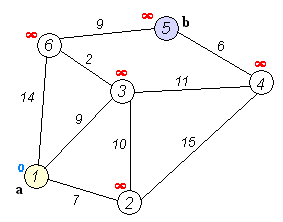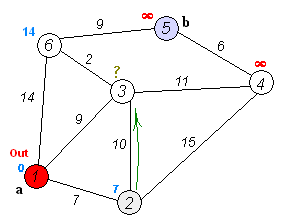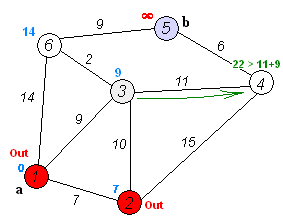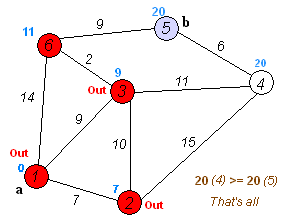
伪代码实现

函数 Dijkstra(图 G, 源节点 source):
    初始化一个距离数组 distance，长度为图中节点的数量
    对于每个节点 v ∈ G:
        distance[v] = ∞  // 初始化为无穷大
    distance[source] = 0  // 源节点到自身的距离为0

    初始化一个优先队列 Q  // 用于存储待处理的节点
    将源节点 source 加入 Q

    当 Q 不为空:
        u = 从 Q 中提取距离最小的节点  // 选择当前最短路径的节点
        从 Q 中移除 u

        对于每个相邻节点 v ∈ G[u]:  // 遍历 u 的所有邻居
            如果 distance[u] + 权重(u, v) < distance[v]:
                distance[v] = distance[u] + 权重(u, v)  // 更新距离
                将 v 加入 Q  // 如果 v 不在 Q 中，则加入 Q

    返回 distance  // 返回源节点到所有其他节点的最短距离