图的拓扑排序

拓扑排序

拓扑排序并不是一类算法，而是针对某一类图（DAG），找到一个可以执行的线性顺序。

DAG 就是有向无环图（Directed acyclic graph）：

1. 图必须是有向图
2. 有向图无环

有以下结论：

• 如果这个图不是 DAG，那么它是没有拓扑序的；
• 如果是 DAG，那么它至少有一个拓扑序；
• 反之，如果它存在一个拓扑序，那么这个图必定是 DAG。

具体定义

在图论中，由一个有向无环图的顶点组成的序列，当且仅当满足下列条件时，才能称为该图的一个拓扑排序：

1. 序列中包含每个顶点，且每个顶点只出现一次；
2. 若 A 在序列中排在 B 的前面，则在图中不存在从 B 到 A 的路径。

AOV 网

AOV（ACtivity on vertex network）网，用于表示事件执行的先后顺序，例如冲豆奶粉的步骤：先烧开水，再冲豆奶粉。

在 AOV 网中，顶点表示事件，弧表示事件间的优先关系，一个 AOV 网必定是一个有向无环图，即不带有回路。与 DAG 不同的是，AOV 的活动都表示在边上。

同时，我们也将 AOV 网表示的序列是一个拓扑排序，因此，拓扑排序也可以解释为将 AOV 网中所有活动排成一个序列，使得每个活动的前驱活动都排在该活动的前面（一个 AOV 网中的拓扑排序也不是唯一的）。

构造拓扑排序

1. 从图中选择一个入度为零的节点。
2. 输出该节点，从图中删除此节点及其所有的出边。

重复上面两步，输出完所有的节点，拓扑排序完成，或者图中不存在入度为零的节点，此时说明图是有环图，拓扑排序无法完成，陷入死锁。

AOE 网

与 AOV 网相对应，存在 AOE 网（Activity on edge network），边表示活动。

AOE 网是一个带权的有向无环图，其中，顶点表示事件，弧表示活动持续的时间，通常用来估算工程的完成时间。

并且存在唯一入度为零的起始顶点（源点），以及唯一出度为零的完成顶点（汇点）。

AOE 网示意图

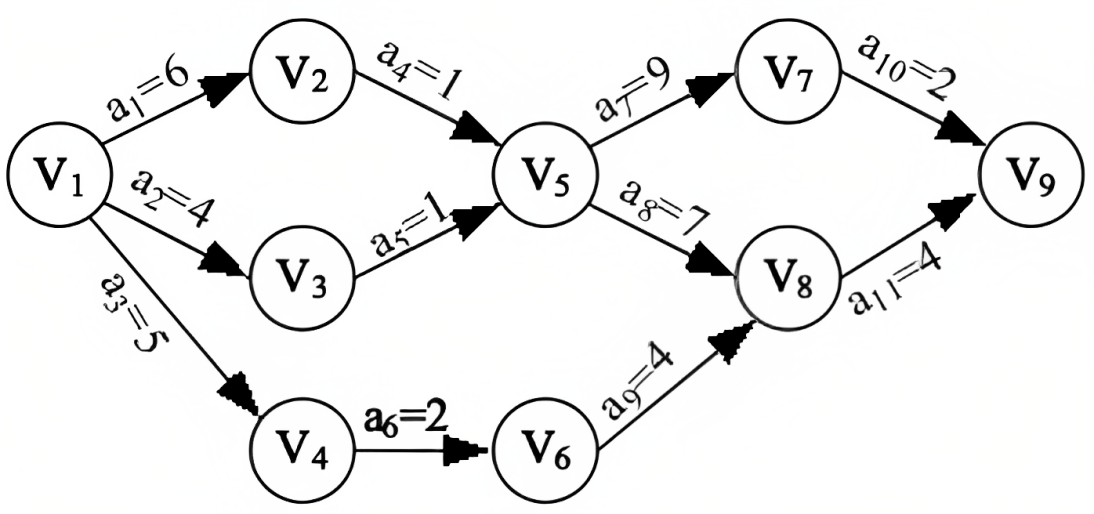
AOE 网中的有些事件是可以并行进行的，所以完成整个工程的最短时间是从开始点到完成点的最长活动路径长度（这里所说的路径长度是指路径上各活动的持续时间之和，即弧的权值之和，不是路径上弧的数目）。

拓扑排序的实现算法

一共两种方案，一种是卡恩（kahn）算法，另一种是深度优先搜索算法！

卡恩（kahn）算法

简单来说，假设L是存放结果的列表，先找到那些入度为零的节点，把这些节点放到L中，因为这些节点没有任何的父节点。

然后把与这些节点相连的边从图中去掉，再寻找图中的入度为零的节点。

对于新找到的这些入度为零的节点来说，他们的父节点已经都在L中了，所以也可以放入L。

重复上述操作，直到找不到入度为零的节点。如果此时L中的元素个数和节点总数相同，说明排序完成；如果L中的元素个数和节点总数不同，说明原图中存在环，无法进行拓扑排序。

• 伪代码实现

  L ← 包含已排序的元素的列表，目前为空
  S ← 入度为零的节点的集合
  当 S 非空时：
      将节点n从S移走
      将n加到L尾部
      选出任意起点为n的边e = (n,m)，移除e。如m没有其它入边，则将m加入S。
      重复上一步。
  如图中有剩余的边则：
      return error   (图中至少有一个环)
  否则：
      return L   (L为图的拓扑排序)

深度优先搜索

深度优先搜索以任意顺序循环遍历图中的每个节点。若搜索进行中碰到之前已经遇到的节点，或碰到叶节点，则中止算法。

• 伪代码实现

  L ← 一个空的 用来存放已排序的节点的列表
  当图中存在未永久标记的节点时：
      选出任何未永久标记的节点n
      visit(n)
  
  function visit(节点 n)
      如n被永久标记：
          return
      如n被临时标记：
          stop   (不是定向无环图，至少有一个环)
  
      将n临时标记
  
      对于每一个以n为起点的边(n,m)：
          visit(m)
  
      去掉n的临时标记
      将n永久标记
      在L的起始位置插入n（如L已有内容 后移它们以空出起始位置）